$\DeclareMathOperator * {\scup}{\cup} \DeclareMathOperator * {\scap}{\cap} $
位相空間論の開集合や連続写像についての例題を解きましたので解答を載せていきます.
定義は最低限しか書いてませんが,細かなことや定理については以下の本を参照しています.

- 作者: 内田伏一
- 出版社/メーカー: 裳華房
- 発売日: 1986/11/01
- メディア: 単行本
- 購入: 4人 クリック: 32回
- この商品を含むブログ (18件) を見る
目次
- 定義
- 4点集合の位相にならない例
- 4点位相空間の部分集合の内部と閉包
- 5点集合の位相空間
- 位相空間の部分集合の差集合
- 位相空間の閉包
- 実数全体 $ \mathbb{R} $ の位相の例
- 自然数全体 $ \mathbb{N} $ の位相の例
- 位相空間の部分集合の開集合・閉集合
- 2次元ユークリッド空間の部分集合の位相
- 2つの連続関数の大小と $ \mathbb{ R } $ の開集合
- 2次正方行列全体の集合について
定義
集合 $ X $ に対し,その部分集合族 $ \mathcal{ O } $ が次の3条件を満たすとき, $ \mathcal{ O } $ は $ X $ の位相であるという. $ (X,\mathcal{ O }) $ を位相空間と呼ぶ.
(1) $ \emptyset \in \mathcal{ O } , X \in \mathcal{ O } $
(2) $ O _ 1,O _ 2 \in \mathcal{ O } ~\Rightarrow ~ O _ 1 \cap O _ 2 \in \mathcal{ O } $
(3) $ \mathcal{ O } $ の元からなる任意の集合族 $ \{O _ \lambda\} _ {\lambda\in \Lambda} $ に対して, $\displaystyle \scup _ {\lambda\in \Lambda} O _ \lambda \in \mathcal{ O } $ .
位相空間 $ X $ の部分集合 $ A $ に対し, $ A $ の内部 $ \operatorname{Int}A $ を, $ A $ に含まれる最大の開集合として定義する.
また, $ A $ の閉包 $ \bar{A} $ を, $ A $ を含む最小の閉集合として定義する.
$ \mathcal{ O } _ A := \{A \cap U | U \in \mathcal{ O } \} $ は $ A $ の部分集合族として位相の3条件を満たす. $ \mathcal{ O } _ A $ の $ A $ 上の $ \mathcal{ O } $ に関する相対位相という.
2つの位相空間 $ (X,\mathcal{ O } _ X),(Y,\mathcal{ O } _ Y) $ と写像 $ f:X\to Y $ に対し,
$ f $ が点 $ x \in X$ で連続である. $ \overset{\mathrm{def}}{\Leftrightarrow} $ 点 $ f(x) \in Y $ の任意の近傍 $ V $ に対して, $ x $ の近傍 $ U $ s.t. $ f(U) \subset V $ が存在する.
4点集合の位相にならない例
4つの元からなる集合 $ X=\{a,b,c,d\} $ を考える.
$ X $ の部分集合族 $ \mathcal{O} := \{ \emptyset , \{ a \} , \{ a , b \} , \{ a , c\} , \{ c , d \} , X \} $ は $ X $ の位相ではない.
なぜなら, $ \{a\} \cup \{ c , d \} =\{a, c , d \}\notin \mathcal{O} $ であるからである.
4点位相空間の部分集合の内部と閉包
4つの元からなる集合 $ X=\{a,b,c,d\} $ と,これに位相 $ \mathcal{O} := \{ \emptyset , \{ a \} , \{ d \} , \{ a , d \} , \{ b , c \} , \{ a , b , c \} , \{ b , c , d \} , X \} $ を入れた位相空間 $ (X,\mathcal{O}) $ を考える.
この位相空間 $ (X,\mathcal{O}) $ の閉集合は全部で $ \emptyset , \{ a \} , \{ d \} , \{ a , d \} , \{ b , c \} , \{ a , b , c \} , \{ b , c , d \} , X $ である.
このとき,集合 $ A=\{a,b\} $ の内部 $ \operatorname{Int}A $ と閉包 $ \bar{A} $ を考える.
$ A $ に含まれる最大の開集合は $ \{a\} $ なので $ \operatorname{Int}A= \{a\}$ である.
$ A $ を含む最小の閉集合は $ \{ a , b , c \} $ なので $ \bar{A}=\{ a , b , c \} $ である.
5点集合の位相空間
5点集合 $ X=\{1,2,3,4,5\} $ と,これに位相 $ \mathcal { O } = \{ \emptyset , \{ 1 \} , \{ 2 \} , \{ 1,2 \} , \{ 1,3 \} , \{ 1,2,3 \} , X \} $ を入れた位相空間 $ (X,\mathcal{O}) $ を考える.
この位相空間 $ (X,\mathcal{O}) $ の開集合は全部で $ \emptyset , \{ 1 \} , \{ 2 \} , \{ 1,2 \} , \{ 1,3 \} , \{ 1,2,3 \} , X $ であり,
閉集合は全部で $ \emptyset , \{4,5\},\{2,4,5\},\{3,4,5\},\{1,3,4,5\},\{2,3,4,5\} , X $ である.
$ \{4\} $ の近傍は $ X $ のみである.
$ A=\{1,3,4\} $ に対し, $ A $ が含んでいる最大の開集合は $ \{1,3\} $ なので $ \operatorname{Int}A=\{1,3\} $ である.
そして, $ A $ を含んでいる最小の閉集合は $ \{1,3,4,5\} $ なので $ \bar{A}=\{1,3,4,5\} $ である.
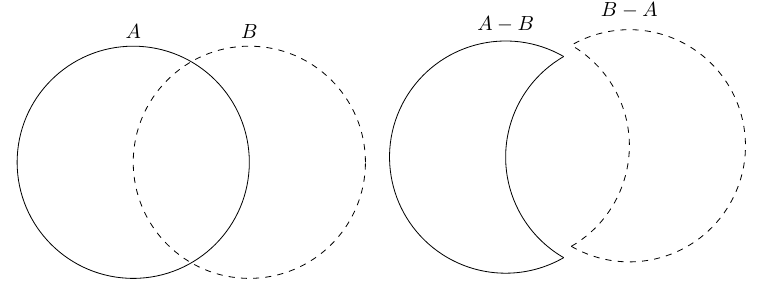
位相空間の部分集合の差集合
$ X $ を位相空間, $ A,B $ を $ X $ の部分集合とし, $ A \cap B \neq \emptyset $ とする. また, $ A $ は閉集合, $ B $ は開集合であるとする.
このとき,集合 $ A-B $ は閉集合であり,集合 $ B-A $ は開集合である.
証明
$ X $ の位相を $ \mathcal{ O } $ とすると, $ (A-B) ^ c=(A\cap B ^ c) ^ c =A ^ c \cup B \in \mathcal{ O } $ なので $ A-B $ は閉集合である. そして $ B-A=B\cap A ^ c \in \mathcal{ O } $ なので $ B-A $ は開集合である.
位相空間の閉包
$ X $ を位相空間で, $ A,B $ を $ X $ の開集合, $ C $ を $ X $ の閉集合とする.
このとき, $ A \subset C $ ならば, $ \bar{A}\subset C $ であり, $ A \cap B = \emptyset $ ならば, $ \bar{A} \cap B = \emptyset $ である.


証明
$ A $ の閉包 $ \bar{A} $ は $ A $ を含む最小の閉集合だから, $ \bar{A}\subset C $ である.
$ A \cap B = \emptyset $ を仮定した時, $ A\subset B ^ c $ である.よって先ほど述べた通り $ \bar{A}\subset B ^ c $ である.すなわち $ \bar{A} \cap B = \emptyset $ である.
実数全体 $ \mathbb{R} $ の位相の例
実数全体 $ \mathbb{R} $ の部分集合族 $ \mathcal { O } = \{ ( a , + \infty ) | a \in \mathbb { R } \} \cup \{ \emptyset , \mathbb { R } \} $ は, $ \mathbb{R} $ の位相になる.
この位相 $ \mathcal{O} $ に対して, $ A=[-1,1] $ の内部と閉包は, $ \operatorname{Int}A=\emptyset ~,~ \bar{A}=(-\infty,1]$ である.
次に,部分集合 $ B=\{1,2,3\} \subset \mathbb{ R } $ に, $ \mathcal{ O } $ を用いて $ B $ 上の相対位相 $ \mathcal{ O } _ B $ を考える.
位相空間 $ (B,\mathcal{ O } _ B) $ の開集合は全部で $ \emptyset , \{3\}, \{2,3\} ,B $ であり, 閉集合は全部で $ \emptyset , \{1\}, \{1,2\} ,B $ である.

証明
定義より $ \emptyset,\mathbb{ R }\in \mathcal{ O } $ である.
任意の $ x _ 1,x _ 2 \in \mathbb{ R } ~(x _ 1<x _ 2) $ に対して, $ (x _ 1,\infty) \cap (x _ 2,\infty) = (x _ 2,\infty) \in \mathcal{ O } $ である.
そして, $ (x _ 1,\infty) \cap \emptyset =\emptyset \in \mathcal{ O } ~,~ (x _ 1,\infty) \cap \mathbb{ R } = (x _ 1,\infty) \in \mathcal{ O } $ である.
$ \mathcal{ O } $ の任意の部分集合 $ \{(\lambda,\infty)\} _ {\lambda\in \Lambda \subset \mathbb{ R }} $ に対して, $ \Lambda $ が非有界のとき, $ \displaystyle \scup _ {\lambda\in \Lambda} (\lambda,\infty) = (-\infty,\infty)=\mathbb{ R } \in \mathcal{ O } $ である.
$ \Lambda $ が有界のとき, $ \displaystyle \scup _ {\lambda\in \Lambda} (\lambda,\infty) = (\inf \lambda,\infty) \in \mathcal{ O } $ である.
以上より, $ \mathcal{ O } $ は $ \mathbb{ R } $ の位相となることが言える.
$ A $ に含まれる最大の開集合は $ \emptyset $ なので $ \operatorname{Int}A=\emptyset $ である.
位相空間 $ (\mathbb{ R },\mathcal{ O }) $ の閉集合全体は $ \{(-\infty,a] | a\in \mathbb{ R }\} \cup \{ \emptyset , \mathbb { R } \} $ である.
よって, $ A $ を含む最小の閉集合は $ (-\infty,1] $ なので, $ \bar{A}= (-\infty,1]$ である.
$ \mathcal { O } = \underbrace{\{ ( a , + \infty ) | a < 1 \}} _ {=:\mathcal { O } _ 0} \cup \underbrace{\{ ( a , + \infty ) | 1 \le a < 2 \}} _ {=:\mathcal { O } _ 1} \cup \underbrace{\{ ( a , + \infty ) | 2\le a < 3\}} _ {=:\mathcal { O } _ 2} \cup \underbrace{\{ ( a , + \infty ) | 3 \le a \}} _ {=:\mathcal { O } _ 3} \cup \{ \emptyset , \mathbb { R } \} $ と分けて考えると,相対位相の定義から
である.
自然数全体 $ \mathbb{N} $ の位相の例
自然数全体の集合 $ \mathbb{N} $ の部分集合族 $ \mathcal { O } = \{ U \subseteq \mathbb { N } | \mathbb { N } - U は有限集合 \} \cup \{\emptyset \} $ は $ \mathbb{ N } $ の位相となる.ただし, $ \emptyset $ は有限集合であると考える.
この位相 $ \mathcal{O} $ に対して, $ A = \{ n \in \mathbb { N } | n \geq 5 \} $ の内部と閉包は, $ \operatorname{Int}A = \emptyset,\bar{A}= \mathbb { N } $ である.

証明
$ \emptyset \in \mathcal{ O } $ である.
$ \mathbb{ N } - \mathbb{ N } = \emptyset$ は有限集合なので $ \mathbb{ N } \in \mathcal{ O } $ である.
任意の $ U _ 1,U _ 2 \in \mathcal{ O } $ に対して, $ \mathbb{ N } - (U _ 1 \cap U _ 2) = \underbrace{(\mathbb{ N } - U _ 1)} _ {有限集合} \cup \underbrace{(\mathbb{ N } - U _ 2)} _ {有限集合} $ が有限集合なので, $ U _ 1 \cap U _ 2 \in \mathcal{ O } $ である.
また, $ \emptyset \cap U _ 1 = \emptyset \in \mathcal{ O } $ である.
$ \mathcal{ O } $ の任意の部分集合 $ \{U _ \lambda\} _ {\lambda \in \Lambda} $ に対して, $ \displaystyle \mathbb{ N } - \bigl ( \scup _ {\lambda\in\Lambda} U _ \lambda \bigr ) = \scap _ {\lambda\in\Lambda} \underbrace{(\mathbb{ N } - U _ \lambda)} _ {有限集合} $は有限集合なので, $ \displaystyle \scup _ {\lambda\in\Lambda} U _ \lambda \in \mathcal{ O } $ である.
以上より, $ \mathcal{ O } $ は $ \mathbb{ N } $ の位相となることが言える.
$ A $ に含まれる最大の開集合は $ \emptyset $ なので $ \operatorname{Int}A=\emptyset $ である.
位相空間 $ (\mathbb{ N },\mathcal{ O }) $ の閉集合全体は $$\{ F \subseteq \mathbb{ N } | \mathbb{ N }-F \in \mathcal{ O } \} = \{ F \subseteq \mathbb{ N } | \mathbb{ N }-(\mathbb{ N }-F)=F が有限集合 \} \cup \{\mathbb{ N } \} $$
である.
$ A $ を含む最小の閉集合は $ \mathbb{ N } $ であるので,$ \bar{A}=\mathbb{ N } $ である.
位相空間の部分集合の開集合・閉集合
位相空間 $ (X,\mathcal{ O }) $ の部分集合 $ A $ に対して,その相対位相 $ \mathcal{ O } _ A $ を入れた位相空間 $ (A,\mathcal{ O } _ A) $ を考える.
(1) $ A $ が $ (X,\mathcal{ O }) $ の開集合であるとき, $ (A,\mathcal{ O } _ A) $ での開集合は $ (X,\mathcal{ O }) $ の開集合でもある.
(2) $ A $ が $ (X,\mathcal{ O }) $ の閉集合であるとき, $ (A,\mathcal{ O } _ A) $ での閉集合は $ (X,\mathcal{ O }) $ の閉集合でもある.
証明
(1) $ (A,\mathcal{ O } _ A) $ の任意の開集合 $ O _ A $ に対し,相対位相 $ \mathcal{ O } _ A $ の定義より $ ^ \exists U \in \mathcal{ O } $ s.t. $ O _ A = A\cap U $ である.
今, $ A \in \mathcal{ O }$ であるから,位相 $ \mathcal{ O } $ の定義より $ O _ A = A\cap U \in \mathcal{ O } $ である.
(2) $ (A,\mathcal{ O } _ A) $ の任意の閉集合 $ F _ A $ に対し, $ A-F _ A \in \mathcal{ O } _ A $ である.
よって,相対位相 $ \mathcal{ O } _ A $ の定義より $ ^ \exists V \in \mathcal{ O } $ s.t. $ A-F _ A = A\cap V $ である.
$ F _ A = A - (A- F _ A) =A-(A\cap V) = \underbrace{(A-A)} _ {=\emptyset} \cup (A-V) = A-V $ より,
$ A $ は $(X,\mathcal{ O }) $ の閉集合, $ V $ は $ (X,\mathcal{ O }) $ の開集合であるから, $ F _ A = A-V $ は $ \mathcal{ O } $ の閉集合である.

2次元ユークリッド空間の部分集合の位相
2次元ユークリッド空間 $ \mathbb{ R } ^ 2 $ 内の部分集合 $ A = \{ ( x , 0 ) \in \mathbb { R } ^ { 2 } | x \in \mathbb { R } \} $ を $ \mathbb{ R } ^ 2 $ の通常の位相による相対位相を考えることで部分位相空間として考える.このとき, $ A $ の部分集合 $ B = \{ ( x , 0 ) \in \mathbb { R } ^ { 2 } | - 1 < x < 1 \} $ は $ A $ の位相で開集合となる.
証明
$ V:= \{(x,y) \in \mathbb{ R } ^ 2 | -1<x<1,-1<y<1\} $ は $ \mathbb{ R } ^ 2$ の通常の位相で開集合である.
$ B = A \cap V $ なので, $ B $ は $ A $ の位相で開集合である.

2つの連続関数の大小と $ \mathbb{ R } $ の開集合
$ f(x),g(x) $ を実数全体 $ \mathbb{ R } $ で定義された連続関数とする.
このとき, $ A= \{x \in \mathbb{ R } | f(x) > g(x)\} $ は $ \mathbb{ R } $ 上の開集合である.
ただし, $ \mathbb{ R } $ の位相は通常の位相で考える.
証明
$ h(x) = f(x)-g(x) ~( ^ \forall x\in \mathbb{ R }) $ とする. $ f,g $ は連続関数なので $ h $ も連続関数である.
$ A' := \{y \in \mathbb{ R } | y>0\} $ は $ \mathbb{ R } $ 上で開集合である.
$ h $ が連続関数なので $ h ^ {-1}(A')=\{x \in \mathbb{ R } | h(x) \in A'\} $ は $ \mathbb{ R } $ 上の開集合である.
よって $ A = \{x \in \mathbb{ R } | f(x) - g(x)>0\} = \{x \in \mathbb{ R } | h(x)>0\} = \{x \in \mathbb{ R } | h(x) \in A'\}= h ^ {-1}(A') $ は $ \mathbb{ R } $ 上の開集合である.
2次正方行列全体の集合について
実数を成分に持つ2次正方行列全体の集合を $ M(2,\mathbb{ R }) $ とする. $ M(2,\mathbb{ R }) $ の4つの成分を4次元ユークリッド空間 $ \mathbb{ R } ^ 4 $ の成分とみなすことで, $ M(2,\mathbb{ R }) $ に $ \mathbb{ R } ^ 4 $ の通常の位相を考える.このとき,
(1) 正則2次正方行列全体の集合 $ GL _ 2(\mathbb{ R }) :=\{A\in M(2,\mathbb{ R }) | \det A \ne 0 \} $ は $ M(2,\mathbb{ R }) $ の開集合となる.
(2) 行列式が1の2次正方行列全体の集合 $ SL _ 2(\mathbb{ R }) :=\{A\in M(2,\mathbb{ R }) | \det A=1 \} $ は $ M(2,\mathbb{ R }) $ の閉集合となる.
証明
(1) 行列に行列式を対応させる関数 $ \det : M(2,\mathbb{ R }) \to \mathbb{ R }$ は連続関数である.
$ \{0\} $ は $ \mathbb{ R } $ の閉集合であり, $ \mathbb{ R }-\{0\} $ は $ \mathbb{ R } $ の開集合である.
よって $ GL _ 2(\mathbb{ R }) =\{A\in M(2,\mathbb{ R }) | \det A \in \mathbb{ R }-\{0\} \} = \det ^ {-1} (\mathbb{ R }-\{0\}) $ は $ M(2,\mathbb{ R }) $ の開集合である.
(2) $ \{1\} $ は $ \mathbb{ R } $ の閉集合なので, $ SL _ 2(\mathbb{ R }) =\{A\in M(2,\mathbb{ R }) | \det A\in \{1 \} \} = \det ^ {-1} (\{1\}) $ は $ M(2,\mathbb{ R }) $ の閉集合である.
