位相空間論のコンパクト性についての例題

位相空間論のコンパクト性についての例題を解きましたので，解答を載せていきます． $\DeclareMathOperator*{\scup}{\cup}$

目次

定義

位相空間 $ (X,\mathcal{O}) $ 上の部分集合 $ A $ の開被覆とは，開集合族

\begin{equation} \{O _ \lambda \} _ {\lambda\in\Lambda} \subset \mathcal{O} ~\mathrm{s.t.}~ A \subset \bigcup _ {\lambda\in\Lambda} O _ \lambda \end{equation}

のことをいう． $ \Lambda $ が有限集合の場合，有限開被覆という．

---

位相空間 $ (X,\mathcal{O}) $ 上の部分集合 $ A $ がコンパクト(集合)である．

⇕def

$ A $ の任意の開被覆 $ \{U _ \lambda \} _ {\lambda\in\Lambda} $ に対して，有限個の添え字

\begin{equation} \lambda _ 1 ,\cdots, \lambda _ n \in \Lambda ~\mathrm{s.t.}~ A \subset \bigcup ^ n _ {i=1} U _ {\lambda _ i} \end{equation}

が存在する．

(i.e. 任意の開被覆が有限部分開被覆を持つ)

とくに全空間 $ X $ がコンパクトの時， $ (X,\mathcal{O}) $ をコンパクト空間という．

・対偶

$ A $ がコンパクト集合ではない．

⇕

$ A $ の開被覆 $ \{U _ \lambda \} _ {\lambda\in\Lambda} $ で，その有限部分集合 $ \{U _ {\lambda _ i} \} _ {i=1} ^ n ~(\lambda _ i\in\Lambda) $ の全てが $\displaystyle A \not\subset \scup _ {i=1} ^ n U _ i $ となるものが存在する． (i.e. 有限部分被覆ができない開被覆が存在する．)

---

集合 $ X $ に対し， $\{\emptyset,X\} $ は $ X $ の位相となり， $ (X, \{\emptyset,X\} ) $ を密着空間という．

---

・ハイネ―ボレルの定理

$ n $ 次元ユークリッド空間の部分集合 $ K $ がコンパクトである．⇔ $ K $ は有界閉集合である．

コンパクトではない集合の例

1次元ユークリッド空間 $ \mathbb{R} $ 内の開区間 $ A=(0,1) $ はコンパクトではない．

・証明

開区間 $ O _ n := (0, 1-\frac{1}{n}) $ は任意の $ n\in \mathbb{N} $ において $ \mathbb{R} $ の開集合であり，

\begin{equation} A \subset \bigcup _ {n\in\mathbb{N}} O _ n \end{equation}

なので， $ \{O _ n\} _ {n\in\mathbb{N}} $ は $ A $ の開被覆である．

しかし，この開被覆 $ \{O _ n\} _ {n\in\mathbb{N}} $ のどんな有限部分集合を取っても $ A $ を被覆することはできない．

実際，任意の有限部分集合 $ \{O _ {n _ i}\} _ {i=1} ^ n ~(n _ i \in \mathbb{N})$ は，

\begin{equation} 1- \frac{1}{2\max _ i\{ n _ i\}} \in A \end{equation}

を含まない，

よって， $ A $ はコンパクトではないことが言える．

▶TikZコード

\usetikzlibrary{calc}
\begin{tikzpicture}
%On
\draw (0,0) -- (.1,.3) -- node[above] { $ O _ n $ } (2,.3) -- (2.1,0);
%A
\draw (0,0) node[below] {0} --  (5,0)  node[below] {1} node[right] { $ A $ };
\filldraw[fill=white] (0,0) circle (2pt);
\filldraw[fill=white] (5,0) circle (2pt);
%Onの点
\filldraw[fill=white] (2.1,0) node[below] { $ 1-\frac{1}{n} $ } circle (2pt);
\fill ( $ (2.1,0)!.5!(5,0) $ ) node[below] { $ 1-\frac{1}{2n} $ } circle (1pt);
\end{tikzpicture}

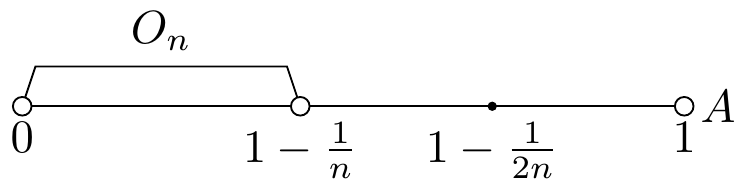
n次元ユークリッド空間 $ \mathbb{R} ^ n $ はコンパクトではない

開球 $ B _ n(0;m) := \{ x\in \mathbb{R} ^ n ~|~ d(0,x) < m \} $ は開集合である．

$ \{B _ n(0,m)\} _ {m\in\mathbb{N} } $ は $ \mathbb{R} ^ n $ を被覆する．

しかし， $ \{B _ n(0,m)\} _ {m\in\mathbb{N} } $ のどんな有限部分集合をとっても $ \mathbb{R} ^ n $ を被覆することはできない．

よって， $ \mathbb{R} ^ n $ はコンパクトではないことが言える．

密着空間 $ (X, \{\emptyset,X \} ) $ はすべての部分集合がコンパクトである

空でない部分集合 $ A \subset X $ に対し，この開被覆は全部で $ \{X\} , \{\emptyset,X\} $ である．これはどちらも有限被覆である．

$ A=\emptyset $ の場合は， $ A $ の開被覆は $ \{\emptyset\} , \{X\}, \{\emptyset,X\} $ である．これらは全て有限被覆である．

よって，任意の $ A\subset X $ はコンパクトである．

2つのコンパクト集合の和集合もコンパクト集合である

位相空間 $ X $ のコンパクト集合 $ K _ 1,K _ 2 $ と，その和集合 $ K:= K _ 1 \cup K _ 2 $ を考える．

$ K $ の任意の開被覆 $ \{U _ \lambda\} _ {\lambda\in \Lambda} $ は $ K _ 1,K _ 2 $ の開被覆でもある．

$ K _ 1,K _ 2 $ のコンパクト性より， $ K _ 1 $ の有限被覆 $ \{ U _ {\lambda _ i} \} _ {i=1} ^ n ~(\lambda _ i \in \Lambda) $ と， $ K _ 2 $ の有限被覆 $ \{ U _ {\lambda _ i} \} _ {i=n+1} ^ m ~(\lambda _ i\in \Lambda) $ が存在する．

$\displaystyle K \subset \scup _ {i=1} ^ m U _ {\lambda _ i} $ である．

よって $ K $ はコンパクトである．

コンパクト空間の閉部分集合はコンパクトである．

コンパクト空間 $ X $ の閉部分集合 $ F $ の任意の開被覆 $ \{U _ \lambda\} _ {\lambda\in\Lambda} $ を考える．

$ F $ の補集合 $ F ^ c := X-F $ は開集合であり， $\{ \{U _ \lambda\} _ {\lambda\in\Lambda} , F ^ c \}$ は $ X $ の開被覆となる．

$ X $ のコンパクト性より， $ X $ の有限被覆 $ \{\{ U _ {\lambda _ i} \} _ {i=1} ^ n , F ^ c\} ~(\lambda _ i \in \Lambda)$ が存在する．

よって

\begin{equation} F \subset X \subset (\scup _ {i=1} ^ n U _ {\lambda _ i}) \cup F ^ c \end{equation}

なので，

\begin{align} F &= F \cap F \\ &\subset \left ((\scup _ {i=1} ^ n U _ {\lambda _ i}) \cup F ^ c \right ) \cap F = \Bigr (\scup _ {i=1} ^ n (\underbrace{U _ {\lambda _ i} \cap F} _ {\subset U _ {\lambda _ i}}) \Bigr ) \cup \underbrace{(F ^ c\cap F)} _ {=\emptyset} \\ &\subset \scup _ {i=1} ^ n U _ {\lambda _ i} \end{align}

である．よって $ \{ U _ {\lambda _ i} \} _ {i=1} ^ n $ は $ F $ の有限被覆である．

よって， $ F $ はコンパクトである．

▶TikZコード

\begin{tikzpicture}
\node[above right] at (1.5,1.5) { $ X $ };
\fill[gray,opacity=0.1] (-2,-2) rectangle (2,2);
\draw[dashed] (0,0) circle (1);
\node[above] at (0,1) { $ \{U _ \lambda\} _ {\lambda\in\Lambda} $ };
\draw (0,0) circle (0.75);
\node at (0,0) { $ F $ };
\node at (1,-1) { $ F ^ c $ };
\end{tikzpicture}

直交行列全体の集合はコンパクトである．

実数を成分に持つ2次正方行列全体の集合を $ M(2,\mathbb{ R }) $ とする． $ M(2,\mathbb{ R }) $ の4つの成分を4次元ユークリッド空間 $ \mathbb{ R } ^ 4 $ の成分とみなすことで， $ M(2,\mathbb{ R }) $ に $ \mathbb{ R } ^ 4 $ の通常の位相を考える．

$ O _ 2(\mathbb{ R }) $ を2次直交行列全体の集合としたとき，この集合は $ M(2,\mathbb{ R }) $ のコンパクト集合になる．

・証明

直交行列を $ T = \begin{pmatrix}x & y \\ z & w\end{pmatrix} $ とする．

直交行列の条件より，

\begin{align} \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix} = { ^ tT} T = \begin{pmatrix}x & z \\ y & w\end{pmatrix} \begin{pmatrix}x & y \\ z & w\end{pmatrix} =\begin{pmatrix}x ^ 2 +z ^ 2 & xy+zw \\ xy+zw & y ^ 2+w ^ 2\end{pmatrix} \end{align}

より， $ x ^ 2 +z ^ 2 = y ^ 2+w ^ 2 =1 ~\Rightarrow ~ x ^ 2 + y ^ 2+z ^ 2 +w ^ 2 =2 $ である．

すなわち，

\begin{align} O _ 2(\mathbb{ R }) &=\{ T \in M(2,\mathbb{ R }) ~|~ { ^ tT}T = T{ ^ tT} =I \} \\ &= \{ (x,y,z,w) \in \mathbb{ R } ^ 4 ~|~ x ^ 2 +z ^ 2 = y ^ 2+w ^ 2 =1 , xy+zw=0 \} \\ &\subset \{ (x,y,z,w) \in \mathbb{ R } ^ 4 ~|~ x ^ 2 + y ^ 2+z ^ 2 +w ^ 2 =2 , xy+zw=0 \} \\ &\subset S ^ 3 \end{align}

である．3次元球面 $ S ^ 3 $ は有界閉集合なのでハイネ―ボレルの定理よりコンパクトである．

そして， $ S ^ 3 $ の閉部分集合 $ O _ 2(\mathbb{ R }) $ もコンパクトである．

閉区間[0,1]と開区間(0,1)は同相ではない

1次元ユークリッド空間 $ \mathbb{R} $ 内の部分集合に通常の位相の相対位相をあたえて考える．

このとき，閉区間[0,1]と開区間(0,1)は同相ではない．

・証明

$ [0,1] \simeq (0,1) $ と仮定する．

よって，同相写像 $ f : [0,1] \to (0,1) $ が存在する．

[0,1] は $ \mathbb{R} $ 内の有界閉集合なので，ハイネ―ボレルの定理より [0,1] はコンパクトである．

よって， $ (0,1) = f([0,1]) $ はコンパクトである．

しかし，実際は (0,1) はコンパクトではないので矛盾する．

よって， $ [0,1] \not\simeq (0,1) $ である．

閉区間[0,1]と1次元ユークリッド空間 $ \mathbb{R} $ は同相ではない

$ [0,1] \simeq \mathbb{R} $ と仮定する．

よって，同相写像 $ f : [0,1] \to \mathbb{R} $ が存在する．

[0,1] は $ \mathbb{R} $ 内の有界閉集合なので，ハイネ―ボレルの定理より [0,1] はコンパクトである．

よって， $ \mathbb{R} = f([0,1]) $ はコンパクトである．

しかし，実際は $ \mathbb{R} $ はコンパクトではないので矛盾する．

よって， $ [0,1] \not\simeq \mathbb{R} $ である．

1次元ユークリッド空間 $ \mathbb{R} $ がコンパクトにならない位相の例

実数全体 $ \mathbb{R} $ の部分集合族 $ \mathcal { O } = \{ ( a , + \infty ) | a \in \mathbb { R } \} \cup \{ \emptyset , \mathbb { R } \} $ は， $ \mathbb{R} $ の位相になる．

参考 位相空間の開集合・閉集合・連続写像の例題 - 三浦と窮理とブログ

この位相空間 $ (\mathbb{ R },\mathcal{ O }) $ はコンパクトではない．

・証明

$ \{( a , + \infty )\} _ {a\in\mathbb{ R }} $ は $ \mathbb{ R } $ の開被覆である．

しかし， $ \{( a , + \infty )\} _ {a\in\mathbb{ R }} $ からどんな有限部分集合をとっても $ \mathbb{ R } $ を被覆することはできない．

実際，任意の有限部分集合 $ \{( a _ i , + \infty )\} _ {i=1} ^ n ~(a _ i\in\mathbb{ R }) $ に対して， $\displaystyle \min _ i \{a _ i\} -1 \notin \scup _ {i=1} ^ n ( a _ i , + \infty ) $ である．

特殊線形群 $ SL _ 2(\mathbb{ R} ) $ はコンパクトではない

実数を成分に持つ2次正方行列全体の集合を $ M(2,\mathbb{ R }) $ とする． $ M(2,\mathbb{ R }) $ の4つの成分を4次元ユークリッド空間 $ \mathbb{ R } ^ 4 $ の成分とみなすことで， $ M(2,\mathbb{ R }) $ に $ \mathbb{ R } ^ 4 $ の通常の位相を考える．

$ \mathbb{ R } ^ 4 $ にはユークリッド距離 $ d $ を与えるとする．

このとき， $ SL _ 2(\mathbb{ R }) $ は非有界なのでハイネ―ボレルの定理より $ \mathbb{ R } ^ 4 $ のコンパクト集合ではない．

すなわち， $ SL _ 2(\mathbb{ R }) $ は $ M(2,\mathbb{ R }) $ のコンパクト集合ではない．

・非有界性の証明

任意の実数 $ M>0 $ に対して， $ P(M) := \begin{pmatrix}M & 0 \\ 0 & \frac{1}{M}\end{pmatrix} \in SL _ 2(\mathbb{ R }) $ は， $ d(0,P) = \sqrt{M ^ 2 + \frac{1}{M ^ 2} } >M $ である．

よって任意の半径 $ M $ よりも原点から遠い元 $ P(M) \in SL _ 2(\mathbb{ R }) $ が存在するので， $ SL _ 2(\mathbb{ R }) $ は非有界である．