単一量子ビットゲート の練習問題3の回答です。
問題文
Y基底で測定する関数を作成してみてください。
直観的回答
QiskitのQuantumCircuit.measure はZ基底による測定をしますので、Y基底によって測定したような結果を得るためには QuantumCircuit.measure による測定前にY基底をZ基底に変換する必要があります。
ブロッホ球で考えてみます。$ |\circlearrowleft\rangle$ を $ |0\rangle$ に変換するゲートを探します。
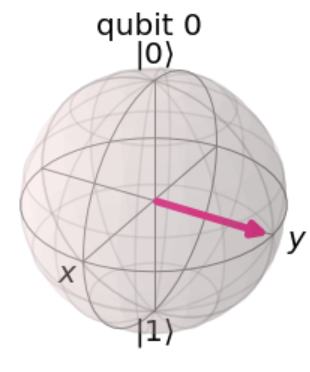
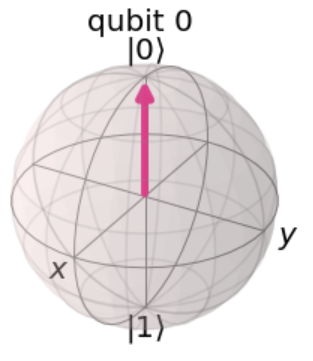
それを実現するゲートの1つとしては$ HP(-\pi/2) $ があると思います。$P(\phi)$はPゲートです。
計算による回答
まずはY基底をZ基底で表します。
\begin{align} |\circlearrowleft\rangle &= \frac{1}{\sqrt{2}}(|0\rangle + i|1\rangle) = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ i \end{bmatrix} \\ |\circlearrowright\rangle &= \frac{1}{\sqrt{2}}(|0\rangle - i|1\rangle) = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ -i \end{bmatrix} \end{align}
Y基底をZ基底に変換するユニタリゲートをAと置きますと次の式が成り立ちます。
\begin{align} A|\circlearrowleft\rangle &= |0\rangle \\ A|\circlearrowright\rangle &= |1\rangle \end{align}
2つの式を行列表記にしてまとめてしまうと、
\begin{align} A \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ i & -i \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \end{align}
よって
\begin{align}
A
= \sqrt{2}\begin{bmatrix} 1 & 1 \\ i & -i \end{bmatrix}^{-1}
= \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -i \\ 1 & i \end{bmatrix}
= \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & -i \end{bmatrix}
= H P(- \pi / 2)
\end{align}
です。
Python関数で表すと以下です。
# Y測定関数を作成します。 def y_measurement(qc, qubit, cbit): """Measure 'qubit' in the Y-basis, and store the result in 'cbit'""" qc.p(-pi/2, qubit) # qc.sdg(qubit) でも可 qc.h(qubit) qc.measure(qubit, cbit) return qc