備忘録として量子計算の公式をまとめていきます。(随時更新)
記法は基本的にQiskitを使った量子計算の学習 を参考にしています。
記法
| 記法 | メモ | |
|---|---|---|
| Z基底 | $|0\rangle, |1\rangle$ | |
| X基底 | $|+\rangle, |-\rangle$ | |
| Y基底 | $|\circlearrowleft\rangle, |\circlearrowright\rangle$ | |
| ビットのXOR演算子 | $\oplus$ | |
| $|q_n...q_1q_0\rangle$の第 $i$ 量子ビットが制御ビット、第 $j$ 量子ビットが標的ビットのCNOTゲート | $\text{CNOT}_{ij}$ | その他の制御ゲートも同様の添え字を付けます。 |
公式
| 公式 | メモ | |
|---|---|---|
| ブロッホ球表現 | $ |q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle $ | $\theta$: zx平面の角度、$\phi$: xy平面の角度 |
| 基底変換 |
$|\pm\rangle = \tfrac{1}{\sqrt{2}}(|0\rangle \pm |1\rangle) = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ \pm 1 \end{bmatrix}$ $|\circlearrowleft\rangle = \frac{1}{\sqrt{2}}(|0\rangle + i|1\rangle) = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ i \end{bmatrix}$ $|\circlearrowright\rangle = \frac{1}{\sqrt{2}}(|0\rangle - i|1\rangle) = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ -i \end{bmatrix}$ |
|
| Xゲート |
$X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$ $X^{-1} = X$ $X|0\rangle = |1\rangle, X|1\rangle = |0\rangle$ |
|
| Yゲート |
$Y = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}$ $Y|0\rangle = i|1\rangle, Y|1\rangle = -i|0\rangle$ |
|
| Zゲート |
$Z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$ $Z|0\rangle = |0\rangle, Z|1\rangle = -|1\rangle$ $Z|\pm\rangle = |\mp\rangle$ |
|
| アダマールゲート |
$H = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$ $H^{-1} = H$ $H|0\rangle = |+\rangle, H|1\rangle = |-\rangle$ $H|+\rangle = |0\rangle, H|-\rangle = |1\rangle$ $X = HZH$ $H = |+\rangle\langle0|~+~ |-\rangle\langle1| = |0\rangle\langle+|~+~ |1\rangle\langle-|$ |
X,Z基底の相互変換 ブロッホ球のx軸とz軸の間の線を中心とする回転 |
| Pゲート | $P(\phi) = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\phi} \end{bmatrix}$ |
ブロッホ球のZ軸回転 $P(\psi)|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i(\phi + \psi)}\sin{\tfrac{\theta}{2}}|1\rangle $ X→Y基底変換 $P(\pi/2)$ Y→X基底変換 $P(-\pi/2)$ Y→Z基底変換 $HP(-\pi/2)$ |
| Sゲート($\sqrt{Z}$ゲート) |
$S = \begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}, \quad S^\dagger = \begin{bmatrix} 1 & 0 \\ 0 & -i \end{bmatrix}$ $S = P(-\pi/2)$ $S^2 = Z $ $Y = SXS^\dagger$ |
|
| U3ゲート | $U_3(\theta, \phi, \lambda) = \begin{bmatrix} \cos(\theta/2) & -e^{i\lambda}\sin(\theta/2) \\ e^{i\phi}\sin(\theta/2) & e^{i\lambda+i\phi}\cos(\theta/2) \end{bmatrix}$ | オイラー角 |
| RYゲート | $\begin{align}\begin{aligned}\newcommand{\th}{\frac{\theta}{2}}\\\begin{split}RY(\theta) = \exp\left(-i \th Y\right) = \begin{pmatrix} \cos{\th} & -\sin{\th} \\ \sin{\th} & \cos{\th} \end{pmatrix}\end{split}\end{aligned}\end{align}$ | |
| 制御NOTゲート(2量子ビット系) |
$\text{CNOT}_{01} = \begin{bmatrix} 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
\end{bmatrix}$ $\text{CNOT}_{10} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix}$ $CNOT_{01}|q_1q_0\rangle = |(q_1\oplus q_0)q_0\rangle$ $\text{CNOT}_{01}|{-}{+}\rangle = |{-}{-}\rangle$ |
$q_1q_0 = 00,01,10,11$ の基底の順番 $|01\rangle$ と $|11\rangle $ の振幅をスワップする 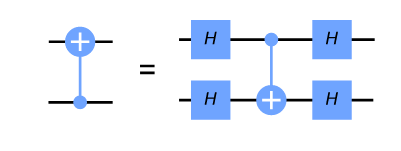
|
| ベル状態 | $\text{CNOT}_{01}|0{+}\rangle = \tfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle)$ | 制御ビットを重ね合わせ状態にしておくともつれる |
| GHZ状態 | $ |GHZ\rangle = \frac{1}{\sqrt{2}}\left( |000\rangle+|111\rangle\right) $ |
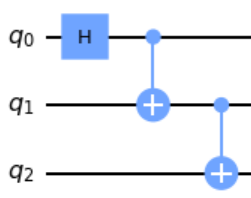
|
| 制御Uゲート |
$\begin{aligned}
\text{U} & =
\begin{bmatrix}
u_{00} & u_{01} \\
u_{10} & u_{11}\\
\end{bmatrix} \\
\quad & \\
\text{Controlled-U}_{10} & =
\begin{bmatrix}
I & 0 \\
0 & U\\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & u_{00} & u_{01} \\
0 & 0 & u_{10} & u_{11}\\
\end{bmatrix}
\end{aligned}$ $\text{Controlled-U}_{01} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & u_{00} & 0 & u_{01} \\ 0 & 0 & 1 & 0 \\ 0 & u_{10} & 0 & u_{11}\\ \end{bmatrix}$ |
|
| 制御Tゲート | $\text{Controlled-T}_{01} = \text{Controlled-T}_{10} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e^{i\pi/4}\\ \end{bmatrix}$ | 制御Pゲートは制御ビット、標的ビットの入れ替えに対して不変 |
| 制御Z |
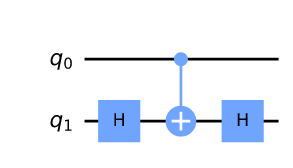 $X = HZH$より |
|
| 制御Y |
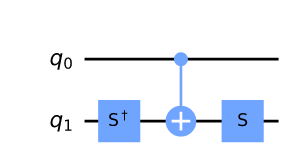 $Y = SXS^\dagger$より |
|
| 制御H |
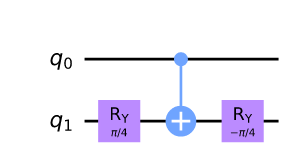 $H=R_Y(-\pi/4)XR_Y(\pi/4)$より |
|
| 制御 RY(θ) |
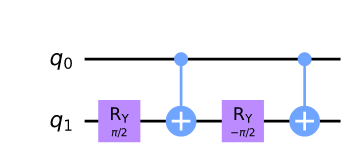 $R_Y(\theta)=XR_Y(-\theta/2)XR_Y(\theta/2)$より |
|
| 制御 RZ(θ) |
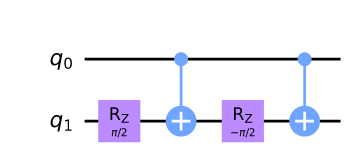 $R_Z(\theta)=XR_Z(-\theta/2)XR_Z(\theta/2)$より |
|
| 制御 RX(θ) |
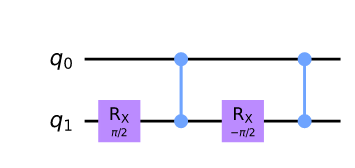 $R_X(\theta)=ZR_X(-\theta/2)ZR_X(\theta/2)$より |
|
| パウリ行列による基底の表現 |
$\frac{1+Z}{2} =|1\rangle\langle1|$ $\frac{1-Z}{2} =|0\rangle\langle0|$ $\frac{X-iY}{2} =|0\rangle\langle1|$ $\frac{X-iY}{2} =|1\rangle\langle0|$ $\left(\frac{1+Z}{2}\right)\otimes\left(\frac{1+Z}{2}\right)\otimes\ldots\otimes\left(\frac{1+Z}{2}\right) = |00\ldots0\rangle\langle00\ldots0|,$ |
|
| ブールオラクル | $U_f |x, \bar{0} \rangle = |x, f(x) \rangle $ | |
| 位相オラクル | $P_f |x\rangle = (-1)^{f(x)} |x\rangle$ | |