前置きの前置き

量子コンピュータについて少し勉強してみたので，量子プログラミング入門という題でまとめていきたいと思います．「現在利用可能な量子コンピュータを触ってみよう」というようなモチベーションです．ハードウェア自体は現在も世界各地で絶賛発展中であり，技術開発についての話題も世間的にはホットらしいですが私は追えてないので本記事でも扱いません．

この記事では量子計算の初歩とIBM製量子プログラミングpythonライブラリのQiskitの概要についての説明をしていきます．この記事を読んで量子プログラミングについての大まかな流れを掴んでいただければいいなと思います．一方でQiskitのチュートリアルが元々分かりやすくできていますのですぐにそちらから始めることもできるでしょう．

この記事はスピン系の量子力学を知っている方ならすぐに理解できるくらいの内容だと思います．スライド形式で要点をまとめたものがあり，口頭で説明すれば1時間かかるくらいの内容量です．

事実の説明に対して私個人の見解もいくつか含まれます．気軽に読んでいただいて，もし致命的な間違いなどがあれば教えていただければ幸いです．

前置きの前置き
要点スライド
前置き
量子計算入門
量子プログラミング
別リンク

要点スライド

Introduction qc from koutarmiur

前置き

まずは最近話題になったニュースについて触れたいと思います．『量子超越性を実証した』というGoogleの発表についてです． 量子超越性とは，古典コンピュータでは実用的な時間ではどうしても解けない問題(タスク)の中に，量子コンピューターで実際に解けるものがあることを指します．

Googleの発表によりますと，Googleが開発している53qubits超電導量子コンピュータを用いて，53ビット文字列(整数)のランダムサンプリングを200秒間で100万回実行できたそうです．それは最新の古典的なスパコンでも1万年かかるタスクだそうです*1．この53ビット整数の出現確率分布はレーザーによる量子的な干渉によって作られた一様ではない分布*2であって，これは古典コンピュータでシミュレーションするのはとても難しいそうです．

確率分布からのランダムサンプリングは古典的には時間のかかるタスクですが，このタスクは量子物理的には量子状態の観測実験そのものです．後ほど説明するようにこのタスクは量子コンピュータの基本機能そのものです．Googleが発表したこの結果は量子コンピュータの基本的な操作の精度・実行速度が着実に急速に発展していることを示すとても重要な結果だと思います．

f:id:OviskoutaR:20191120093353j:plain

量子コンピュータとは何かを大雑把に言ってしまいますと，量子コンピュータとは量子状態の生成・観測をプログラマブルに自動化してくれる装置 であると言えると思います．とくに汎用量子コンピュータと言われる量子ゲート方式について私は勉強したのですが，そのような特徴をもとに量子アルゴリズムが考えられているようです．ハードウェア技術的には難しくて今も発展途上ですが，機能自体は素朴であるので，数論・組み合わせ問題・機械学習など様々な応用先がすでに研究されています．

f:id:OviskoutaR:20191120093551j:plain

量子計算入門

多ビット状態はそれらのテンソル積で表されています．例えば2つの量子ビット$x _ 0, x _ 1$がある系は $|x _ 0 \rangle \otimes |x _ 1\rangle = |x _ 0 x _ 1\rangle $という固有状態で張られます．(合成スピンの固有状態表示をするとビット描像ができなくなるのでその議論は扱われません．しかし量子力学の教科書にあるような角運動量合成の議論の中で，実験できそうなところを量子コンピュータで試してみるのも面白そうです．合成スピンを使えばスピン1の系を量子コンピュータで扱うこともできそうな気がします．)

量子計算とは量子状態にユニタリ変換をしていくことを言います．このユニタリ変換を量子ゲートと呼びます．

このユニタリ変換の順序を表した図を量子回路図と呼びます．（量子回路図はあくまでユニタリ変換の順序を表した図なので，電気回路のように素子同士の接続状況を表したものではありません．）

例えば初期状態 $|0\rangle$ にアダマールゲートを作用させて重ね合わせ状態 $\frac{1}{\sqrt{2}}[|0\rangle + |1\rangle]$を生成する過程を次のスライドにあるような図で表します．

f:id:OviskoutaR:20191120093803j:plain

量子ゲートにはいろいろな種類が知られています．特に，万能ゲートと呼ばれる，これがあればどんなユニタリ変換でもできるという量子ゲートの組があります．それは，1qubit位相回転ゲート と 2qubits制御NOTゲートです．

他にも名前の付いた量子ゲートがたくさんありますが，そのすべての変換は位相回転ゲートと制御NOTゲートの組み合わせによって実現することができます．1qubitゲートは全て1qubit位相回転ゲートに含まれますし，マルチqubits ゲートも制御NOTゲートとの組み合わせで構成できます．

f:id:OviskoutaR:20191120093900j:plain

最後に量子コンピュータで得られる計算結果について説明します．量子コンピュータでは最終的に，ユニタリ変換後の量子状態の観測結果を知ることができます．量子回路を設定したら，その回路を何度も実行して状態生成・観測を繰り返し，観測された状態の回数をカウントしてくれます．

例えば，先ほど扱ったアダマール変換回路を1000回実行することで，『$|0\rangle$ が496回，$|1\rangle$ が504回観測された．』というような結果が得られます．ヒストグラムを使って，相対確率を図示することができます．

以上のように初期状態$|initial\rangle$にユニタリ変換Uを作用させた状態 $U|initial\rangle$ の観測をするというのが量子コンピュータの基本操作となります．

例えば量子ゲートを使って特定のハミルトニアンの時間発展演算子を構成できれば実際にスピン系の物理シミュレーションを行うこともできます．（ハードウェアが量子的なのでそれはもはや量子物理実験と言えると思います．）今ではクラウドで量子コンピュータが無料公開されていますから，実験装置を自前で持たずとも量子的モデルの実験ができるというのは画期的なことだと思います．これから量子力学を学習する学生は教科書に書いてある量子現象を実際に量子コンピュータで実験しながら勉強することができると考えると，良い時代になったな思います．

f:id:OviskoutaR:20191120093920j:plain

量子プログラミング

量子計算についての説明は以上になります．ここからは具体的に量子プログラミングについての説明をしていきます．量子プログラミングはライブラリや言語がすでにいろいろ公開されていて，好きなものを選んで使うことができます．

私はIBMが公開しているpythonライブラリのQiskitを使ってみました．量子ゲートがあらかじめいろいろ用意されていて，それらを使った量子回路作成，32qubitsマシンのシミュレーション実行ができます．そしてクラウド経由で量子コンピュータ実機を使用することも可能です．チュートリアルが豊富にありますので入門しやすいと思います．

f:id:OviskoutaR:20191120093941j:plain

Qiskitにある量子ゲートは，API documentation にもあるように現在31種類の量子ゲートが実装されています．その中でも万能ゲートの1つである位相回転ゲートは実際にはU3Gate として次のように定義されていることが確認できます *3．

\begin{equation} U _ 3 (\theta, \phi, \lambda) = \begin{pmatrix} \cos \frac{\theta}{2} & - e ^ {i\lambda} \sin \frac{\theta}{2} \\ e ^ {i\phi} \sin \frac{\theta}{2} & e ^ {i(\phi+ \lambda)} \cos \frac{\theta}{2} \end{pmatrix} \end{equation}

そのほかの1qubitゲートは U3Gate のパラメタに値を代入することで実装されています．

万能ゲートのもう一方であるCNOTゲートは CnotGate として次のようにして定義されていることが確認できます．

\begin{equation} CNOT = \begin{pmatrix} 1 &&& \\ &0&& 1 \\ &&1& \\ &1&&0 \end{pmatrix} \end{equation}

これは2qubitsゲートなのですが， Qiskitでは最下位ビットを左側に定義しています *4．よって，0,1,2,3 はそれぞれ2進数で 00, 10, 01, 11 と表されていて，この CnotGate は左側のビットを制御ビット，右側のビットをターゲットビットとしています．このゲートは制御ビットが 1 の時にターゲットビットに NOT 動作をしてくれます．

少し余談ですが，実は教科書的には別の定義が主流だそうで，最下位ビットを右側に定義するそうです．この表示では 0, 1, 2, 3 はそれぞれ 00, 01, 10, 11 と表されます．この場合，左側のビットを制御ビットする CNOT ゲートの行列表示は

\begin{equation} CNOT = \begin{pmatrix} 1 &&& \\ &1&& \\ &&0&1 \\ &&1&0 \end{pmatrix} \end{equation}

となります．

f:id:OviskoutaR:20191120093959j:plain

ちなみにこの位相回転ゲート U3Gate はSU(2)回転を表していますが，次のようにパラメータを代入すれば教科書でよく見るようなリー群の元の形にもなります．これらはそれぞれ RXGate, RYGate, RZGate として実装されています．

\begin{align} U _ 3 (\theta, -\frac{\pi}{2}, \frac{\pi}{2}) &= \begin{pmatrix} \cos \frac{\theta}{2} & - i\sin \frac{\theta}{2} \\ -i \sin \frac{\theta}{2} & \cos \frac{\theta}{2} \end{pmatrix} = \textbf{1} \cos \frac{\theta}{2} -i X \sin \frac{\theta}{2} = \exp \left( - \frac{i\theta}{2} X \right) \\ U _ 3 (\theta, 0, 0) &= \begin{pmatrix} \cos \frac{\theta}{2} & - \sin \frac{\theta}{2} \\ \sin \frac{\theta}{2} & \cos \frac{\theta}{2} \end{pmatrix} = \exp \left( - \frac{i\theta}{2} Y \right) \\ U _ 1 (\lambda) &= \begin{pmatrix} 1 & 0 \\ 0 & e ^ {i\lambda} \end{pmatrix} = e ^ {\frac{i\lambda}{2}} \begin{pmatrix} e ^ {-\frac{i\lambda}{2}}& 0 \\ 0 &e ^ {\frac{i\lambda}{2}} \end{pmatrix} = e ^ {\frac{i\lambda}{2}} \exp \left( - \frac{i\lambda}{2} Z \right) \label{eq:expZ} \end{align}

（式 \eqref{eq:expZ} にある位相因子 $e ^ {\frac{i\lambda}{2}}$ は観測確率には影響しない．）

他にもイジングモデルで現れるようなスピンの積が指数になっている演算子も

\begin{align} \exp \left( -i \frac{\theta}{2} Z \otimes Z \right) &= \exp [ -i \frac{\theta}{2} \begin{pmatrix} 1 &&& \\ &-1&& \\ &&-1& \\ &&&1 \end{pmatrix} ] = \begin{pmatrix} e ^ {-i\theta/2} &&& \\ &e ^ {i\theta/2}&& \\ &&e ^ {i\theta/2}& \\ &&&e ^ {-i\theta/2}\end{pmatrix} \\ &= \begin{pmatrix} 1 &&& \\ &1&& \\ &&0&1 \\ &&1&0 \end{pmatrix} \begin{pmatrix} e ^ {-i\theta/2} &&& \\ &e ^ {i\theta/2}&& \\ &&e ^ {-i\theta/2}& \\ &&&e ^ {i\theta/2}\end{pmatrix} \begin{pmatrix} 1 &&& \\ &1&& \\ &&0&1 \\ &&1&0 \end{pmatrix} \\ &= CNOT \begin{pmatrix} \exp \left( -i \frac{\theta}{2} Z\right)& \\ &\exp \left( -i \frac{\theta}{2} Z \right) \end{pmatrix} CNOT \\ &= CNOT [I \otimes U _ 1 (\theta) ] CNOT \end{align}

と構成できます．次の左図ような回路です．これが1つにまとまった RZZGate もあります(右図)．

f:id:OviskoutaR:20191121103936p:plain f:id:OviskoutaR:20191122220342p:plain

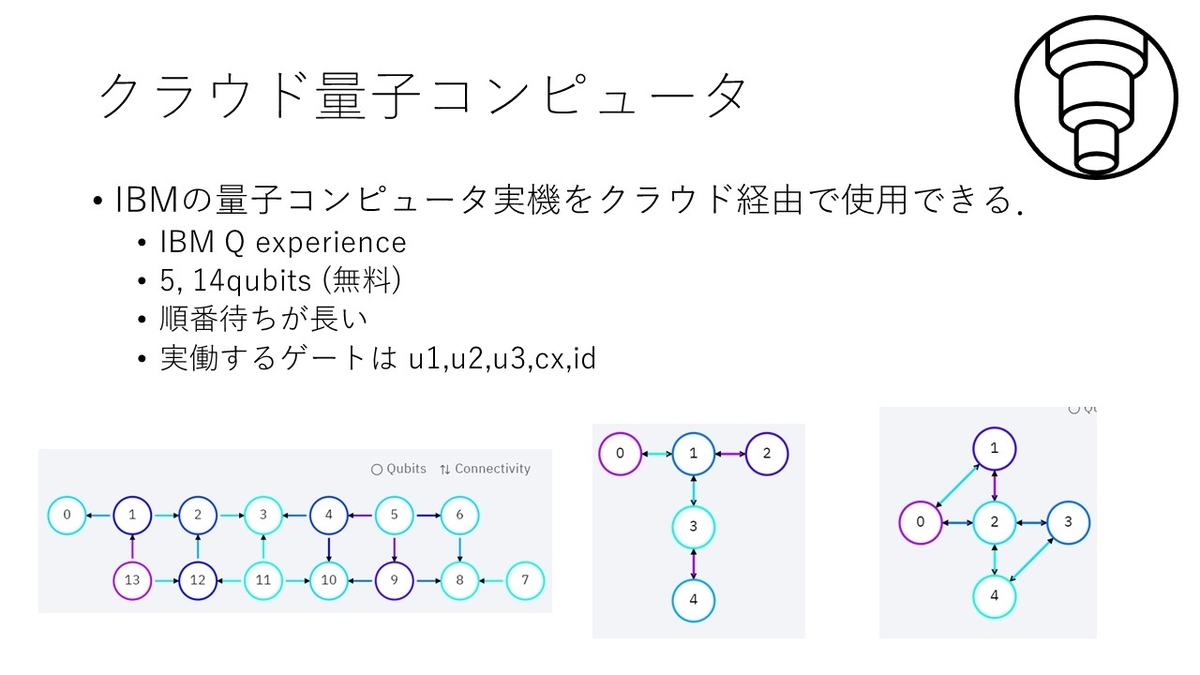
クラウド量子コンピュータは，IBM Q Experience でアカウントを作れば無料公開されているものを使うことができます．現在は5qubitsマシンが6機，14qubitsマシンが1機公開されています．世界中の人が使いますので実行タスクの順番待ちがあります．タスクにもよりますが1タスク1分～10分くらいかかっていた気がします．

f:id:OviskoutaR:20191120094030j:plain

他にもQiskitにはaquaというクラスがあります．そこには有名な量子アルゴリズムのいくつかがすでに実装されていて，関数を実行するようにしてそれらを使うことができます *5．複雑なアルゴリズムは大体，量子計算と古典計算が複合的に使われるのですが，それを一気に実行してくれるので手っ取り早く量子計算を使いたいときにとても便利だと思います．

f:id:OviskoutaR:20191120094039j:plain