量子力学の演習問題シリーズ
次の1次元ポテンシャル中の粒子を考える.
\begin{equation}
V(x) =
\begin{cases}
-V_0 / 2a & |x| < a \\
0 & |x| > a
\end{cases}
\end{equation}
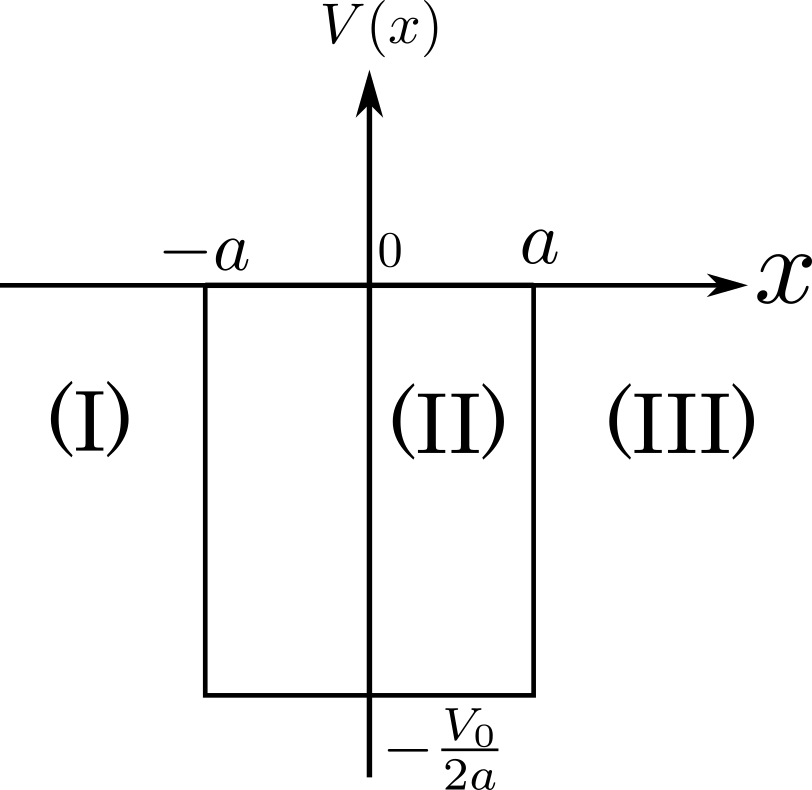
ただし粒子のエネルギー固有値 E を, - V0 / 2a < E < 0 , V0 > 0 , a > 0 とする.ポテンシャルの様子を以下の図に表す.
1次元有限井戸型ポテンシャル
ポテンシャルが偶関数なので,波動関数のパリティは偶または奇であることが言える.本記事では,この系における a → 0 の極限でのエネルギー固有値や波動関数の形について簡単に述べようと思う.実際にこの極限において波動関数の形は偶関数でないといけないことがわかる.
目次
波動関数の一般解
まずはそれぞれの領域においてSchrödinger方程式を解き,波動関数の一般解を示そう.
領域 x < - a における波動関数を ψI (x) とおいた時,Schrödinger方程式は
\begin{equation}
-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} \psi_{\mathrm{I}} (x) = E \psi_I (x)
\end{equation}
である.ψI ( - ∞ ) = 0 と仮定すると,一般解は
\begin{equation}
\psi_{\mathrm{I}} (x) = A e^{k'x} \qquad (Aは任意定数,k'^2:= -\frac{2m}{\hbar^2}E)
\end{equation}
である.
x > a においても同様にして,今度はψIII ( + ∞ ) = 0 となるように波動関数を選ぶと,
\begin{equation}
\psi_{\mathrm{I\hspace{-.1em}I\hspace{-.1em}I}} (x) = B e^{-k'x} \qquad (Bは任意定数)
\end{equation}
となる.
|x| < a において,Schrödinger方程式は
\begin{equation}
-\frac{\hbar^2}{2m} \psi_\mathrm{{I\hspace{-.1em}I}} (x) = (E+\frac{V_0}{2a}) \psi_{\mathrm{I\hspace{-.1em}I}} (x)
\end{equation}
であり,その一般解は,
\begin{equation}
\psi_{\mathrm{I\hspace{-.1em}I}}(x) = C \cos (kx) + D \sin (kx) \qquad (C,Dは任意定数~,~ k^2:=\frac{2m}{\hbar^2}(E+\frac{V_0}{2a}))
\end{equation}
である.以上をまとめるとこのポテンシャル中での波動関数は
\begin{equation}
\psi(x) =
\begin{cases}
\psi_{\mathrm{I}} (x) = A e^{k'x} & x < -a \\
\psi_{\mathrm{I\hspace{-.1em}I}}(x) = C \cos (kx) + D \sin (kx) & |x|< a \\
\psi_{\mathrm{I\hspace{-.1em}I\hspace{-.1em}I}} (x) = B e^{-k'x} & a< x
\end{cases}
\end{equation}
と表される.
k と k' の関係
x = ± a での境界条件より k と k' の間に成立する以下の関係が求まる.
\begin{align}
k' &= -k \cot (ka) \\
k' &= k \tan (ka)
\end{align}
▶クリックで導出を開く
境界条件より,
\begin{alignat}{3}
\psi_{\mathrm{I}} (-a) &= \psi_{\mathrm{I\hspace{-.1em}I}}(-a) \quad&&\Rightarrow\quad & Ae^{-k'a} &= C \cos (ka) - D \sin (ka) \label{eq:12} \\
\frac{d}{dx}\psi_{\mathrm{I}} (-a) &= \frac{d}{dx} \psi_{\mathrm{I\hspace{-.1em}I}}(-a) \quad&&\Rightarrow \quad& k'Ae^{-k'a} &= kC \sin (ka) + k D \cos (ka) \label{eq:d12}\\
\psi_{\mathrm{I\hspace{-.1em}I\hspace{-.1em}I}} (a) &= \psi_{\mathrm{I\hspace{-.1em}I}}(a) \quad&&\Rightarrow\quad & Be^{-k'a} &= C \cos (ka) + D \sin (ka) \label{eq:32}\\
\frac{d}{dx}\psi_{\mathrm{I\hspace{-.1em}I\hspace{-.1em}I}} (a) &= \frac{d}{dx} \psi_{\mathrm{I\hspace{-.1em}I}}(a) \quad&&\Rightarrow \quad& -k'Be^{-k'a} &= -kC \sin (ka) + k D \cos (ka)\label{eq:d32}
\end{alignat}
である.
式\eqref{eq:12}を式\eqref{eq:d12}に代入すると,
\begin{equation}
k'C\cos (ka) - k' D\sin (ka) = kC \sin(ka) + kD\cos(ka) \label{eq:1to2}
\end{equation}
となり,式\eqref{eq:32}を式\eqref{eq:d32}に代入すると,
\begin{equation}
-k'C\cos (ka) - k' D\sin (ka) = -kC \sin(ka) + kD\cos(ka) \label{eq:2to3}
\end{equation}
となる.
式\eqref{eq:1to2}と式\eqref{eq:2to3}を足すと,
\begin{alignat}{2}
&&-k'\sin(ka) &= k \cos (ka) \\
\Leftrightarrow \quad&& k' &= -k \cot (ka)
\end{alignat}
となる.また,式\eqref{eq:1to2} と式\eqref{eq:2to3}を引くと,
\begin{alignat}{2}
&&k'\cos(ka) &= k \sin (ka) \\
\Leftrightarrow \quad&& k' &= k \tan (ka)
\end{alignat}
となる.
a → 0 でのエネルギー固有値と波動関数のふるまい
a → 0 の極限では $ k'=k\underbrace{\tan(ka)}_{\simeq ka} $ より,$ \frac{k'}{k}=ka $ である.
よって,
\begin{equation}
\sqrt{\frac{-E}{E+\frac{V_0}{2a}}} = a \sqrt{\frac{2m}{\hbar^2}(E+\frac{V_0}{2a})}
\end{equation}
であり,更に $ E+\frac{V_0}{2a} \simeq \frac{V_0}{2a} $ という近似をすると,
\begin{equation}
E=-\frac{m{V_0}^2}{2\hbar^2}
\end{equation}
である.
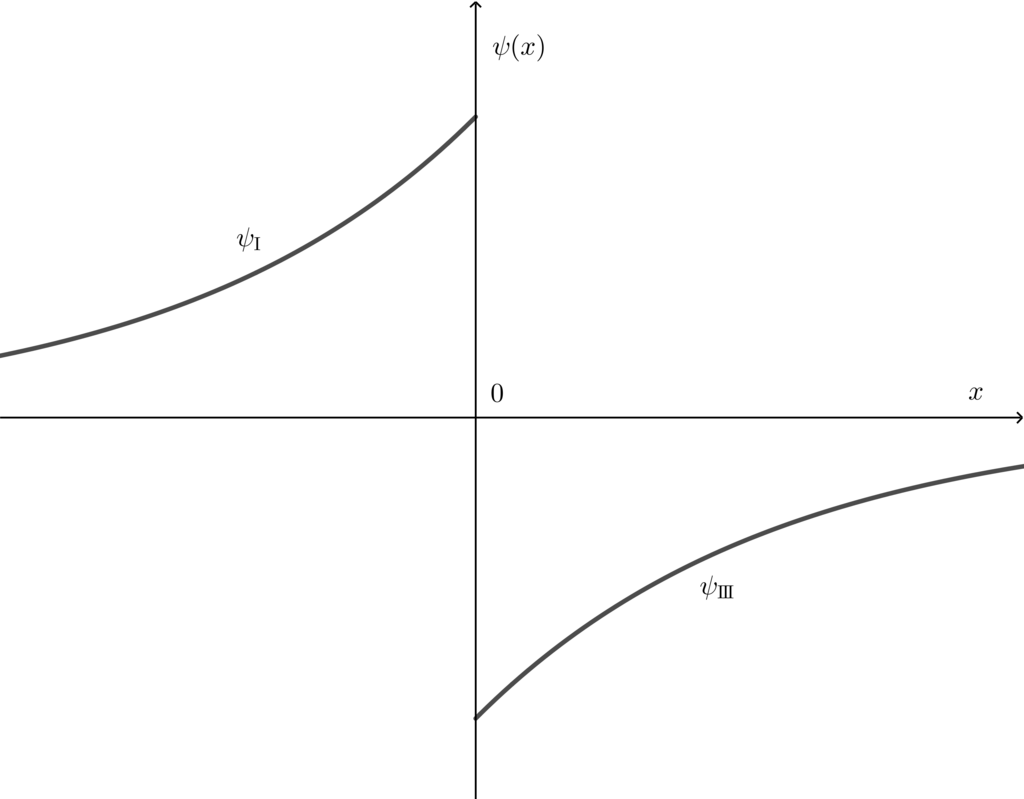
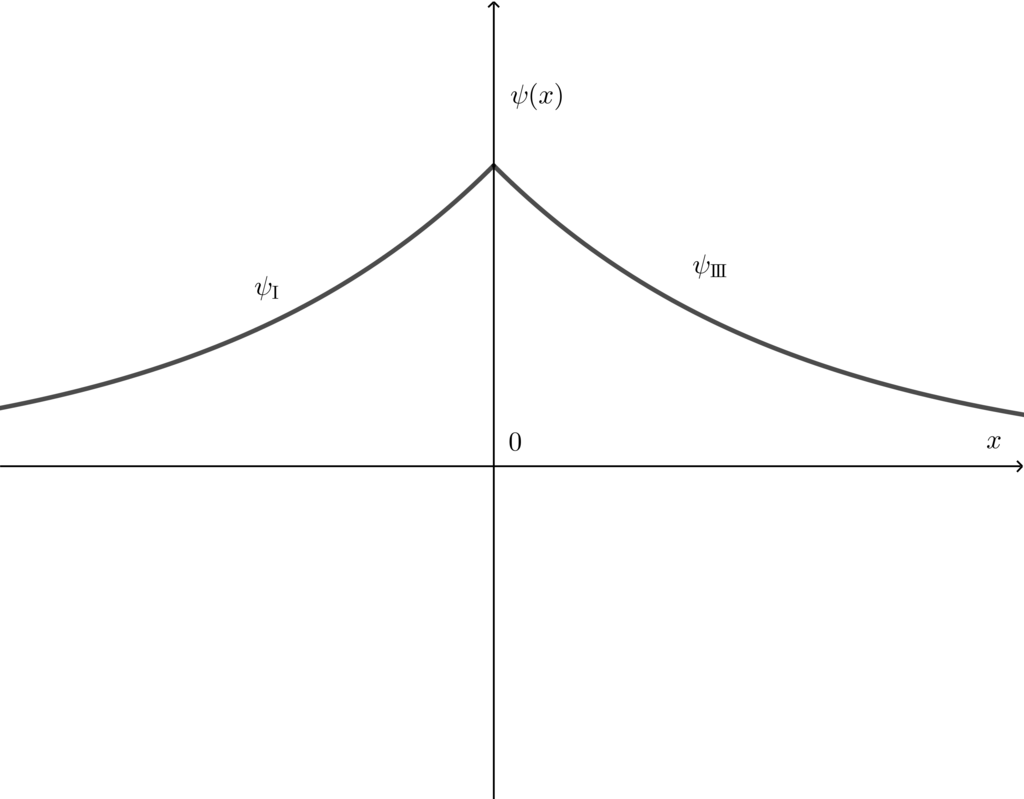
一般に,波動関数の連続性から ψ( -0 ) = ψ( +0 ) が成り立たないといけない.特にa → 0 の極限を考えたときはこの条件は ψI ( -0 ) = ψIII (+0) と書き換えられる.もし波動関数が奇関数の場合はこれに矛盾する.実際に波動関数が奇関数だと仮定した場合, ψ( -x ) = - ψ(x) より,ψI (x) = Aek'x , ψIII (x) = - Aek'x である.しかし a → 0 の極限をとると ψ( -0 ) = ψI ( - 0 ) = A , ψ( +0 ) = ψIII ( +0 ) = - A であり,この波動関数は連続でない.つまり,a → 0 の極限においては波動関数は偶関数でなくてはならない.簡単なイメージ図を以下に示す.
奇関数の場合は極限をとると不連続になる 偶関数なら大丈夫
参考文献