三浦ノート

自分の経験したことを検索可能にしていくブログ．誰かの役に立ってくれれば嬉しいです．

トップ > 数学 > ユークリッド距離空間の開集合についての例題

ユークリッド距離空間の開集合についての例題

数学 位相空間論

ユークリッド距離空間の開集合に関する例題を解いたので共有します．よかったら図もみてください．Tikzのコードも載せてます．

目次

定義

$ n $ 次元ユークリッド空間を $ \mathbb{ R } ^ n $ と表す．

$ \mathbb{ R } ^ n $ の2点 $ x = (x _ 1,\cdots,x _ n) , y =(y _ 1 ,\cdots, y _ n) $ の間の距離を $ d^{(n)}(x,y) = \sqrt{(y _ 1 -x _ 1) ^ 2 + \cdots+(y _ n- x _ n) ^ 2} $ で定義する．

点 $ a \in \mathbb{ R } ^ n $ を中心とした半径 $ \epsilon>0 $ の開球体を $ B _ n (a,\epsilon) = \{x \in \mathbb{ R } ^n | d^{(n)}(a,x) <\epsilon\} $ で定義する．

$ O \subset \mathbb{ R } ^ n $ が開集合である． $\overset{\mathrm{def}}{\Leftrightarrow} { ^ \forall x} \in O , ^ \exists \epsilon >0 $ s.t. $ B _ n (x;\epsilon) \subset O $ ．

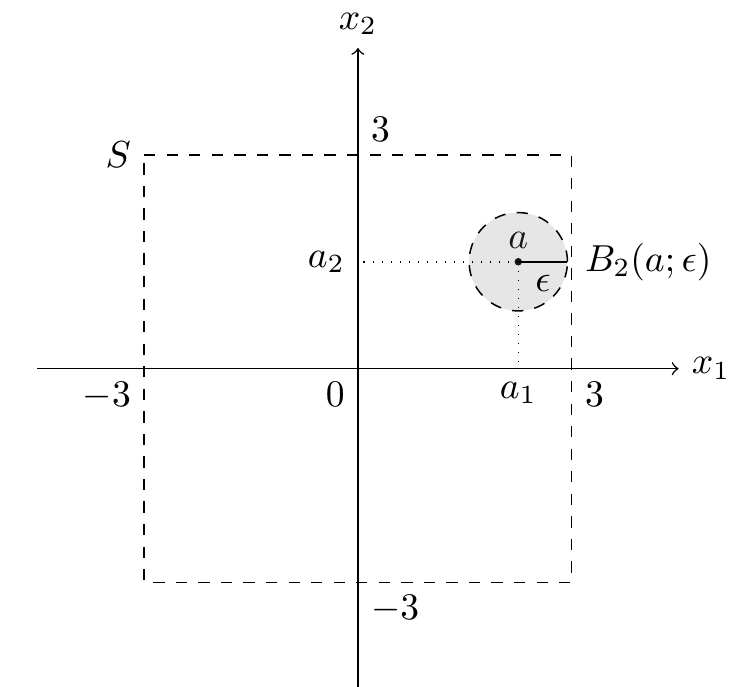
正方形領域$ S = \{( x _ { 1 } , x _ { 2 } ) \in \mathbb { R } ^ { 2 } | | x _ { 1 } | < 3 , | x _ { 2 } | < 3 \} \subset \mathbb { R } ^ { 2 } $ は開集合である

・証明

任意の $ a = (a _ 1, a _ 2) \in S $ に対して，正の数 $ \epsilon \in \mathbb{ R } $ を $ \epsilon < \min\{3- |a _ 1| , 3- |a _ 2|\}$ ととると， $ B _ 2 (a;\epsilon) \subset S $ となる．

実際に，任意の $ x = (x _ 1,x _ 2) \in B _ 2 (a;\epsilon) $ に対して，

\begin{align} \epsilon &> \sqrt{(x_1-a_1)^2 + (x_2-a_2)^2} \ge \sqrt{(x_1-a_1)^2} = |x_1 -a_1| \ge |x_1| - |a_1| \\ \Leftrightarrow\quad |x_1| &< \epsilon + |a_1| < 3- \cancel{|a _ 1| }+ \cancel{|a_1| } \end{align}

である．同様にして $ |x _ 2| < 3 $ なので $ x \in S $ である．つまり，$ B _ 2 (a;\epsilon) \subset S $ である．

以上により $ S $ は $ \mathbb { R } ^ { 2 } $ の開集合である．

f:id:OviskoutaR:20181222012024p:plain:w300

▶Tikzコード

開球 $ B _ n(p;r) $ は開集合である

任意の $ a \in B _ n(p;r) $ に対して，正の数 $ \epsilon $ を $ \epsilon < r- d ^ {(n)}(a,p) $ ととると $ B _ n(a;\epsilon) \subset B _ n (p;r) $ である． 実際，任意の $ x = (x _ 1,x _ 2, \cdots, x _ n) \in B _ n(a;\epsilon) $ に対し，

\begin{equation} d ^ {(n)} (x,p) \le \underbrace{d ^ {(n)}(x,a)} _ {<\epsilon} + \underbrace{d ^ {(n)}(a,p)} _ {< r-\epsilon} < r \end{equation}

より，$ x \in B _ n (p;r) $ である．よって $ B _ n(a;\epsilon) \subset B _ n (p;r) $ である．

以上より $ B _ n(p;r) $ は開集合であることが言えた．

f:id:OviskoutaR:20190101014357p:plain:w300

▶Tikzコード

1点集合は開集合ではない

任意の数 $ \epsilon >0 $ に対して，$ B _ n(p;\epsilon) \nsubseteq \{p\}$ であることを示す．

$ p = (p _ 1,p _ 2,\cdots,p _ n) , q= (p _ 1 + \epsilon/2 ,p _ 2,\cdots,p _ n)$とする． この $ q $ は $ d(p,q) = \epsilon/2 $ より $ q \in B _ n (p;\epsilon) $ であるが，$ q \notin \{p\} $ である． よって $ B _ n(p;\epsilon) \nsubseteq \{p\}$ である．

任意の開集合の和集合は開集合である

$ \mathbb{ R } ^ n $ の開集合全体の成す集合を $ \mathcal{O}(\mathbb{ R } ^ n) $ としたとき， $ \mathcal{O}(\mathbb{ R } ^ n) $ の元からなる任意の集合族 $ \{O _ \lambda\} _ {\lambda \in \Lambda} $ に対して， $ \displaystyle \bigcup _ { \lambda \in \Lambda } O _ { \lambda } \in \mathcal { O } ( \mathbb { R } ^ { n } ) $ である．

・証明

$ O := \displaystyle \bigcup _ { \lambda \in \Lambda } O _ { \lambda } $ と表すとする．

任意の点 $\displaystyle a \in O $ は，$ \{O _ \lambda\} _ {\lambda\in \Lambda} $ の元の中の少なくとも1つに含まれる． その元の一つを $ O _ {\lambda'} $ と表すとする(i.e. $ \lambda'\in \Lambda ,a\in O _ {\lambda'} $)． $ O _ {\lambda'} $ は開集合なので，$ B _ n(a;\epsilon) \subset O _ {\lambda'} $ となる $ \epsilon>0 $ が存在する． $ B _ n(a;\epsilon) \subset O _ {\lambda'} \subset O $ なので $ O $ が開集合であることが示された．

f:id:OviskoutaR:20181222013901p:plain:w300

▶Tikzコード

$ A = \{ ( x , y ) \in \mathbb { R} ^ 2 | y > x \} $ は開集合である

任意の点 $ a = (a _ x,a _ y) \in A $ と直線 $ y=x $ の距離は $ \displaystyle \frac{a _ y -a _ x}{\sqrt{2}} $ である． よって $ \displaystyle \epsilon < \frac{a _ y -a _ x}{\sqrt{2}} $ となる数 $ \epsilon >0 $ をとると，$ B _ 2 (a;\epsilon) \subset A $ となるから $ A $ は開集合であることが言える．

実際，任意の点 $ b = (b _ x,b _ y) \in B _ 2 (a;\epsilon) $ に対して，これを$ r = d ^ {(2)}(a,b) <\epsilon , \tan\theta = \frac{a _ y - b _ y}{a _ x - b _ x} $ という極座標 $ (r,\theta) $ を用いて表すと，

\begin{align} b _ y - b _ x &= (a _ y + r\sin\theta) - (a _ x+r\cos\theta ) = a _ y -a _ x +r(\sin\theta- \cos\theta) \\ &= a _ y -a _ x +r\sqrt{2}\underbrace{\sin(\theta- \frac{3}{4}\pi)} _ {\ge -1} > a _ y -a _ x -\epsilon\sqrt{2} >0 \end{align}

となる．よって $ b \in A $ である．よって $ B _ 2 (a;\epsilon) \subset A $ である．

f:id:OviskoutaR:20181222014009p:plain:w300

▶Tikzコード